MATEMATIKA
A.BANGUN RUANG MATEMATIKA
Rumus Kubus
- Volume : Sisi pertama dikali sisi kedua dikali sisi ketiga (S pangkat 3)
- Volume : Sisi pertama dikali sisi kedua dikali sisi ketiga (S pangkat 3)
Rumus Balok
- Volume : Panjang dikali lebar dikali tinggi (p x l x t)
- Volume : Panjang dikali lebar dikali tinggi (p x l x t)
Rumus Bola
- Volume : phi dikali jari-jari dikali tinggi pangkat tiga kali 4/3 (4/3 x phi x r x t x t x t)
- Luas : phi dikali jari-jari kuadrat dikali empat (4 x phi x r x r)
- Volume : phi dikali jari-jari dikali tinggi pangkat tiga kali 4/3 (4/3 x phi x r x t x t x t)
- Luas : phi dikali jari-jari kuadrat dikali empat (4 x phi x r x r)
Rumus Limas Segi Empat
- Volume : Panjang dikali lebar dikali tinggi dibagi tiga (p x l x t x 1/3)
- Luas : ((p + l) t) + (p x l)
- Volume : Panjang dikali lebar dikali tinggi dibagi tiga (p x l x t x 1/3)
- Luas : ((p + l) t) + (p x l)
Rumus Tabung
- Volume : phi dikali jari-jari dikali jari-jari dikali tinggi (phi x r2 x t)
- Luas : (phi x r x 2) x (t x r)
- Volume : phi dikali jari-jari dikali jari-jari dikali tinggi (phi x r2 x t)
- Luas : (phi x r x 2) x (t x r)
Rumus
Kerucut
- Volume : phi dikali jari-jari dikali jari-jari dikali tinggi dibagi tiga (phi x r2 x t x 1/3)
- Luas : (phi x r) x (S x r)
- S : Sisi miring kerucut dari alas ke puncak (bukan tingi)
- Volume : phi dikali jari-jari dikali jari-jari dikali tinggi dibagi tiga (phi x r2 x t x 1/3)
- Luas : (phi x r) x (S x r)
- S : Sisi miring kerucut dari alas ke puncak (bukan tingi)
Rumus Prisma Segitiga
Siku-siku
- Volume : alas segitiga kali tinggi segitiga kali tinggi prisma bagi dua (as x ts x tp x)
- Volume : alas segitiga kali tinggi segitiga kali tinggi prisma bagi dua (as x ts x tp x)
B. BENTUK PANGKAT
Rumus Bentuk Pangkat, Akar, dan Logaritma
a. Bentuk Pangkat
1). Jika n bilangan bulat positif dan a bilangan real maka a pangkat n didefinisikan sebagai berikut :
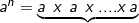
Pengertian pangkat tersebut diperluas, yaitu untuk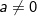 berlaku :
berlaku :
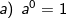
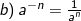
2). Sifat-sifat pengerjaan hitung bilangan berpangkat
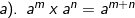
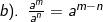
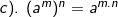
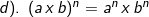
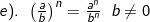
b. Bentuk Akar
1). Jika a dan b bilangan real serta n bilangan bulat positif, maka :
![\inline \fn_cm a).\: \: b^{n}=a\, \Leftrightarrow \,
\sqrt[n]{a}=b](http://latex.codecogs.com/png.latex?%5Cinline%20%5Cfn_cm%20a%29.%5C:%20%5C:%20b%5E%7Bn%7D=a%5C,%20%5CLeftrightarrow%20%5C,%20%5Csqrt[n]%7Ba%7D=b)
![\inline \fn_cm b).\: \: \sqrt[n]{a}=a^{\frac{1}{n}}](http://latex.codecogs.com/png.latex?%5Cinline%20%5Cfn_cm%20b%29.%5C:%20%5C:%20%5Csqrt[n]%7Ba%7D=a%5E%7B%5Cfrac%7B1%7D%7Bn%7D%7D)
2). Sifat-sifat bentuk akar.
![\inline \fn_cm a).\: \: \sqrt[n]{a^{m}}=a^{\frac{m}{n}}](http://latex.codecogs.com/png.latex?%5Cinline%20%5Cfn_cm%20a%29.%5C:%20%5C:%20%5Csqrt[n]%7Ba%5E%7Bm%7D%7D=a%5E%7B%5Cfrac%7Bm%7D%7Bn%7D%7D)
![\inline \fn_cm b).\: \:
p\sqrt[n]{a}+q\sqrt[n]{a}=(p+q)\sqrt[n]{a}](http://latex.codecogs.com/png.latex?%5Cinline%20%5Cfn_cm%20b%29.%5C:%20%5C:%20p%5Csqrt[n]%7Ba%7D+q%5Csqrt[n]%7Ba%7D=%28p+q%29%5Csqrt[n]%7Ba%7D)
![\inline \fn_cm c).\: \:
p\sqrt[n]{a}-q\sqrt[n]{a}=(p-q)\sqrt[n]{a}](http://latex.codecogs.com/png.latex?%5Cinline%20%5Cfn_cm%20c%29.%5C:%20%5C:%20p%5Csqrt[n]%7Ba%7D-q%5Csqrt[n]%7Ba%7D=%28p-q%29%5Csqrt[n]%7Ba%7D)
![\inline \fn_cm d).\: \: \sqrt[n]{a.b}=\sqrt[n]{a}\,\, x\,
\sqrt[n]{b}](http://latex.codecogs.com/png.latex?%5Cinline%20%5Cfn_cm%20d%29.%5C:%20%5C:%20%5Csqrt[n]%7Ba.b%7D=%5Csqrt[n]%7Ba%7D%5C,%5C,%20x%5C,%20%5Csqrt[n]%7Bb%7D)
![\inline \fn_cm e).\: \:
\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\, ,b\neq \neq 0](http://latex.codecogs.com/png.latex?%5Cinline%20%5Cfn_cm%20e%29.%5C:%20%5C:%20%5Csqrt[n]%7B%5Cfrac%7Ba%7D%7Bb%7D%7D=%5Cfrac%7B%5Csqrt[n]%7Ba%7D%7D%7B%5Csqrt[n]%7Bb%7D%7D%5C,%20,b%5Cneq%20%5Cneq%200)
![\inline \fn_cm f).\: \: \sqrt[m]{\sqrt[n]{a}}=\sqrt[m.n]{a}](http://latex.codecogs.com/png.latex?%5Cinline%20%5Cfn_cm%20f%29.%5C:%20%5C:%20%5Csqrt[m]%7B%5Csqrt[n]%7Ba%7D%7D=%5Csqrt[m.n]%7Ba%7D)
3). Merasionalkan penyebut pecahan bentuk akar
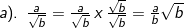
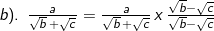
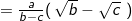
1). Jika n bilangan bulat positif dan a bilangan real maka a pangkat n didefinisikan sebagai berikut :
Pengertian pangkat tersebut diperluas, yaitu untuk
2). Sifat-sifat pengerjaan hitung bilangan berpangkat
b. Bentuk Akar
1). Jika a dan b bilangan real serta n bilangan bulat positif, maka :
2). Sifat-sifat bentuk akar.
3). Merasionalkan penyebut pecahan bentuk akar
c. Logaritma
1).
Jika a dan b bilangan positif dengan 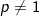 maka berlaku :
maka berlaku :
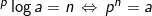
Dari hubungan tersebut, diperoleh :

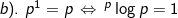

2). Sifat-sifat logaritma
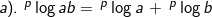
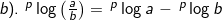
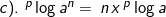
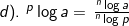
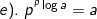
Dari hubungan tersebut, diperoleh :
2). Sifat-sifat logaritma
C. FUNGSI PERSAMAAN
KUADRAT
Bentuk
Umum Persamaan Kuadrat seperti ini
 ,
,  dan a, b, c,
dan a, b, c,
Dimana :
x adalah variabel persamaan kuadrat
a adalah koefisien x kuadrat
b adalah koefisien x
c adalah konstanta
 ,
,  dan a, b, c,
dan a, b, c,
Dimana :
x adalah variabel persamaan kuadrat
a adalah koefisien x kuadrat
b adalah koefisien x
c adalah konstanta
Cara Menyelesaikan Persamaan Kuadrat
1) Mencari faktor

diuraikan menjadi
cara pemfaktoran akan lebih mudah bila a = 1
maka kita bisa menebak x1 dan x2 dengan cara
a = 1
b = x1+x2
c = x1.x2
2) Memakai Rumus Kuadrat atau Rumus abc

3) Melengkapkan Kuadrat Sempurna
Bentuk umum persamaan kuadrat bebentuk kuadrat sempurna adalah :
dengan q > 0
Menentukan Jenis Akar-Akar Persamaan Kuadrat Jenis
akar-akar persamaan kuadrat ditentukan oleh nilai deskriminan :

a. D > 0 Kedua akar nyata dan berlainan,
b. D = 0
Kedua akar nyata dan sama,
c. D <> Kedua akar tidak nyata (imaginer)
d.dengan

bilangan kuadrat sempurna, kedua akar rasional.
Untuk menghitung
jumlah dan hasil kali akar-akar persamaan kuadrat , dapat dicari
tanpa terlebih dahulu mencari akar-akarnya.
Dari rumusdan

Dapat ditunjukkan bahwa:
Rumus-rumus Akar Persamaan Kuadrat hasil pengembangan,
sering sekali muncul di soal UAN SNMPTN atau SPMB
Sifat-sifat Akar Persamaan Kuadrat Jika  dan
dan  adalah akar-akar persamaan kuadrat
adalah akar-akar persamaan kuadrat  dengan
dengan 
 dan
dan  adalah akar-akar persamaan kuadrat
adalah akar-akar persamaan kuadrat  dengan
dengan 
maka berlaku sifat-sifat berikut ini :
a. Syarat mempunyai Dua Akar Positif

b. Syarat mempunyai Dua Akar Negatif

c. Syarat mempunyai Dua Akar Berlainan Tanda

d. Syarat mempunyai Dua Akar Berlawanan

e. Syarat mempunyai kedua akar berkebalikan
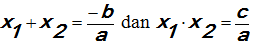








0 komentar:
Posting Komentar